Compute the background#

Reminder

Start the exercise with the Python template file in the src directory corresponding to the exercise.

Your code must be added to the main function.

If you write generic functions, put them into libraries to reuse them easily in other applications. Look at Library and Module documentation for more details on Python libraries.

You should carefully follow the division in steps proposed for every exercise and provide specific signatures for each step when this is specified.

Git operations:

Commit very frequently with relevant message. Focus on making clear the reasons why you made the change.

Push once a significant result is obtained.

Code quality:

Check frequently the PyCharm annotations about your code, for example the colored signals in the right vertical gutter.

Execute the check_commit_status.py script to check the validation tests.

Assess the quality of your code with SonarQube.

Documentation:

Add docstrings (""" ... """) at begining of ALL functions & classes.

Add one-line comments wherever this is useful to understand your code.

Refer to slides for detailed information on technical topics.

Goal#

In order to analyse what is in the image we’ve read, we have to differentiate the signal (stars, galaxies) from the background. This background is made of random pixels (light from terrestrial sky, electronic background, …). In this exercise we’ll evaluate this background.

Principle#

Signal from each of the interesting objects is generally shaped as a gaussian peak in the image. The background is made of random pixels all over the image, yet the global distribution of those pixels values is also shaped as a gaussian. Thus if we analyze the pixel height distribution we see two regions in this distribution:

one gaussian narrow and high peak describing the random background (ie. flat distribution with some statistical dispersion)
a much wider distribution for all celestial objects

Thus in order to extract the background from the pixel distribution, the algorithm is as follows:

from the image (which is a 2D array of pixels), we construct the distribution of all pixel values (this an histogram)
then we apply a dedicated fitting function curve_fit to this distribution to get position and width of the background shape (we exploit the assumption that the background distribution is well separated from the objects pixels)

The fit consists in comparing the pixel values to analyse, with the values given by a modelling function. The modelling function use some formal parameters to describe a formal model, such as - for a gaussian model - the position of the peak, the gaussian width, and the height of the peak.

Then the fit itself will find the best value of all the modelling parameters that minimize the distance between observed values and model values.

Discussion:

Of course, the accuracy of the detection will depend on the threshold value:

high threshold will give cleaner object construction but less object count

low threshold will get more objects with a lower precision

Before completing the following steps, you may want to read again the presentations given on FITS (Fits slides), Numpy Notebook and pyplot (Pyplot slides).

Batch application, step 1: building the pixel distribution#

The batch application steps must be implemented in the file ex2_background.py.

First, reuse the functions developed in the previous exercise to read the image.

Then, build a flat list (1D array) of pixels from the 2D array returned by the function. This is easily done with the numpy.ravel() function:

my1d_array = my2d_array.ravel()

Building the pixel distribution means creating an histogram of the pixel values: each histogram bin accumulates the number of pixels being valued within the bin boundaries. The numpy.histogram() (from numpy module, aliased np in our context) function builds the sample given the number of bins over the effective value range. This function returns two arrays:

the bin values, to be used as \(y\) values
the bin boundaries, to be used to build the bin centers array \(x\), where \(x_i = \frac{1}{2}(boundaries[i]+boundaries[i+1])\)

Hint

Use numpy operations and slicing to easily compute \(x\) values

# build the pixel distribution
bin_values, bin_boundaries = np.histogram(my1D_array, bin_number)

# store the bin values ...
y = bin_values

# ... and compute the bin centers
x = bin_boundaries[:-1]+...

You will have to choose a bin_number so as to obtain a readable histogram. Typical values range from 100 to 1000. You can play with different values to see the effect of the number of bins on the background value. For validating your code in this exercise and for the following ones, you must use 200.

Signature

In order to check the proper construction of the histogram, and deduced \(y\) and \(x\) arrays, we ask you to multiply each \(y\) element with the corresponding \(x\) element, make the sum, and finally divide it by the number of pixels in the original image. Somehow, we are computing the mean pixel value of the image, as approximated by the histogram.

signature_fmt_1 = 'RESULT: histogram = {:.0f}'

If you want to check your program with the common image common.fits, here is the expected signature:

RESULT: histogram = 4775

Batch application, step2: modelling Function#

To prepare the fitting, you need to define a modelling function that describes, in mathematical terms, the analytic model representing your physics model. Generally, this function will depend on several formal parameters and return a value computed with y = f(x, parameters...), f being the modelling function chosen. A typical format for the modelling function is:

def modelling_function(x, p1, p2, p3):
    """
    compute a gaussian function:
    """
    y = ...
    return y

Note that f here is meant to be globally applied to the set of x values, thus the mathematical expression should use the numpy algebra functions (such as numpy.exp()).

The modelling function should return the computed array of values.

In our case, we assume that the modelling function should describe a gaussian distribution with the usual parameters:

p1: the Y maximum value
p2: the X mean value
p3: the standard deviation sigma
Note

There are several ways to express a gaussian function. You might like to experiment different forms and look at what will be the impact of using one forme or another. However, since the very form you use here may induce minor results to the various exercises later on, it’s better to stick on single one conventional form especially to ensure that the signatures for forth coming exercises do match the expected valued.

Therefore you should eventually use the following form:

\[\mathcal{G}(x) = p_1 \exp\left( -\frac{(x - p_2)^2}{2p_3^2} \right)\]

which, when written in Python, gives:
```
max_value * np.exp(-(x - mean_value)**2 / (2 * sigma**2))
```

Signature

In order to check the proper implementation of your modelling function, you should apply it to he following use case:

the input array is given by the linear range np.arange(-3.0, 3.0, 1.0)
the maximum value is 0.5
the mean value is 1.0
the standard deviation sigma is 2.0

Then you should get the array of results and compute its sum and print it as the signature for this step.

signature_fmt_2 = 'RESULT: test_gaussian = {:6f}'

If you want to check your program, whatever the image used, the expected signature is:

RESULT: test_gaussian = 1.915756

Batch application, step3: applying the fit#

The scipy.optimize.curve_fit() function applies a minimization algorithm onto the sampled data, by optimizing the set of formal parameters of the modelling function until the distance between data and the modelling function is minimal.

To help the optimization algorithm we use normalized data, ie. the maximum Y value is 1 and the X values range from 0.0 to 1.0

# normalize the distribution for the gaussian fit
ymax = float(np.max(y))
ynorm = y/ymax
xmax = float(np.max(x))
xnorm = x/xmax

Then we apply the optimization function onto those normalized valued as follows:

fit, covariant = curve_fit(modelling_function, xnorm, ynorm)

Now, we can restore the un-normalized values. Also note that the return fit[2] is sometimes negative, and you should take its absolute value :

maxvalue   = fit[0] * ymax
background = fit[1] * xmax
dispersion = abs(fit[2]) * xmax

Signature

This final signature is made of printing background and dispersion values obtained from the fit function and un-normalized.

The expected formats for this step is:

signature_fmt_3 = 'RESULT: background = {:.0f}'
signature_fmt_4 = 'RESULT: dispersion = {:.0f}'

If you want to check your program with the common image common.fits, here is the expected signature:

RESULT: background = 4326
RESULT: dispersion = 303

If you fail to get the expected signature, it may help to do now the graphic step below wo to visually check what is happening.

Graphic step#

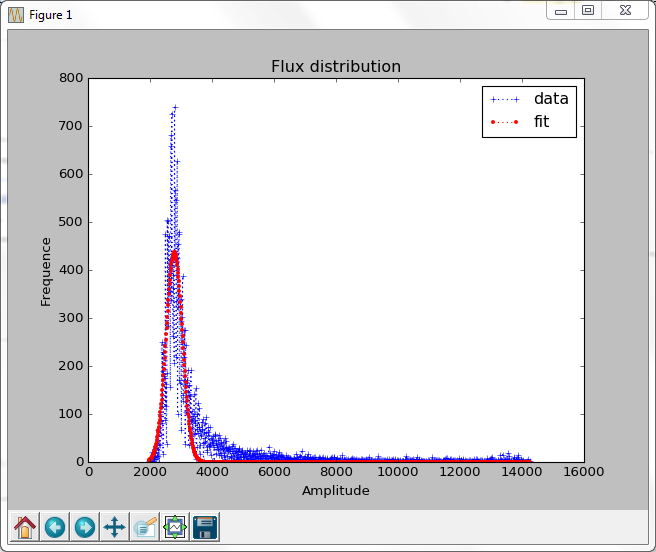
In the display.py application, you are asked to add a new window containing a superposition of the image histogram and the fitted gaussian. Again, refer to the graphics explanations and to the Pyplot slides for details on how to create several windows.

It is again suggested that the work done before, in the previous batch application steps, is move to a specific module, for example lib_background.py. A way to use this module in display.py may be:

import lib_background

# Values returned by compute_background
#   - ``background``: the value of the background for this image
#   - ``dispersion``: the value of the background dispersion for this image
#   - ``(x, y)``: a tuple containing both bin centers and bin values.
background, dispersion, (x, y) = lib_background.compute_background(pixels)

You can plot the histogram using the matplotlib.pyplot.plot() function (be careful that the bin boundary array returned from the histograming function has a size greater than the array of bin values since the boundary array includes the last boundary, thus the ``[:-1]`` slice has to be used):

axes.plot(x, y, 'C1+:', label='data')

Then superpose the fitted gaussian:

axes.plot(x, modelling_function(x, maxvalue, background, dispersion), 'C2.:', label='fit')

Don’t forget to add some labels and legend to your plots (you need to define them for each axis (see graphics explanations and Pyplot slides for details):

axes.legend()
axes.set_title('Flux distribution')
axes.set_xlabel('Amplitude')
axes.set_ylabel('Frequency')

NPAC Computing Course

Compute the background

Contents

Compute the background#

Goal#

Principle#

Batch application, step 1: building the pixel distribution#

Batch application, step2: modelling Function#

Batch application, step3: applying the fit#

Graphic step#